一、相关的含义

客观事物或现象之间有两种数量关系，分别是函数关系和相关关系。当单个或多个变量取固定值时，另一个变量有确定的值与之对应，这种关系为函数关系，可用ｙ=f(x)表示。当事物或现象之间在数量上的变化关系不能直接做出因果关系的解释时，若一个或几个相互间有联系的变量取一定的数值后，在未知的条件下，与之对应的另一个变量同样按照特定的一种规律在某个范围内改变，则称这种关系为相关关系。

相关性分析主要是指对两个以上存在相关关系的变量作定量分析，进而判断两个变量之间的关联程度的方法。如果仅通过传统的表面粗糙度参数来描述工件的表面形貌，不能很好地表征和描述具有三维和空间特征的表面纹理，因此通过相关性分析进行衡量。

二、自相关函数（ACF）

（1）自相关函数简介

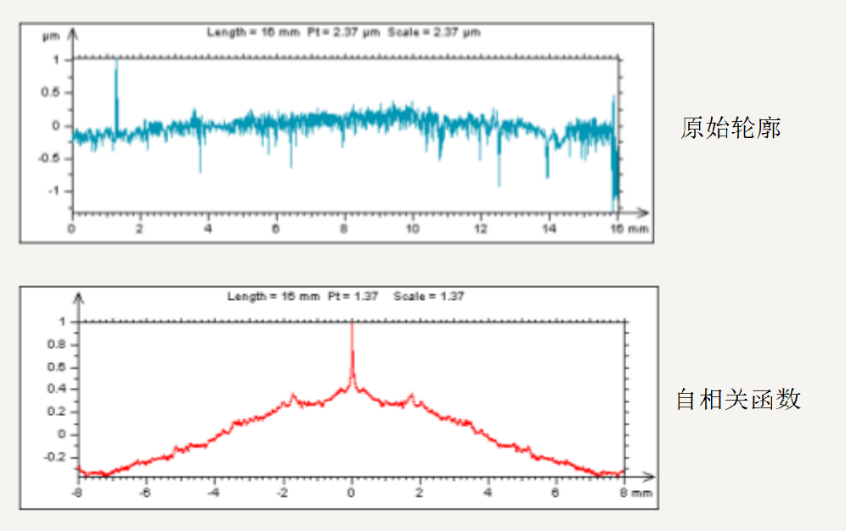
自相关函数（如上图所示）表示同一个轮廓波形相差一定位移时的相似程度。对它们进行自相关函数分析即可反映出表面轮廓的周期性特征，检测出混于轮廓曲线中的周期性成分。

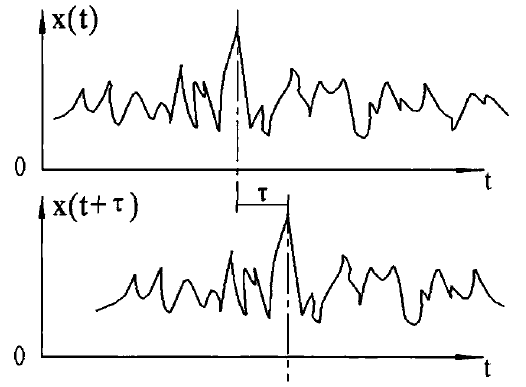
自相关函数的计算公式为：

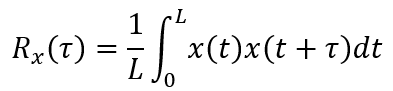
其中，t为沿表面截面轮廓的距离；τ表示横向位移，L表示评定长度。

自相关函数的数字化估算采用直接计算法，当采样长度间距取值为时，结合评定长度L可知，样本容量N=L/h；此处，令横向位移数为r，则横向位移τ＝rh。设m为r的最大值，则横向位移的离散数字序列｛Yn｝(n=0,1,2,…N-1)的自相关函数离散形式ACF(rh)的估计为:

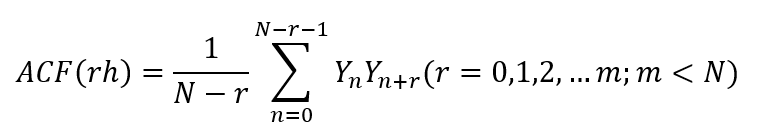
其中，Yn、Yn+r表示第n处和第n+r处表面轮廓的高度。

（2）自相关分析实例

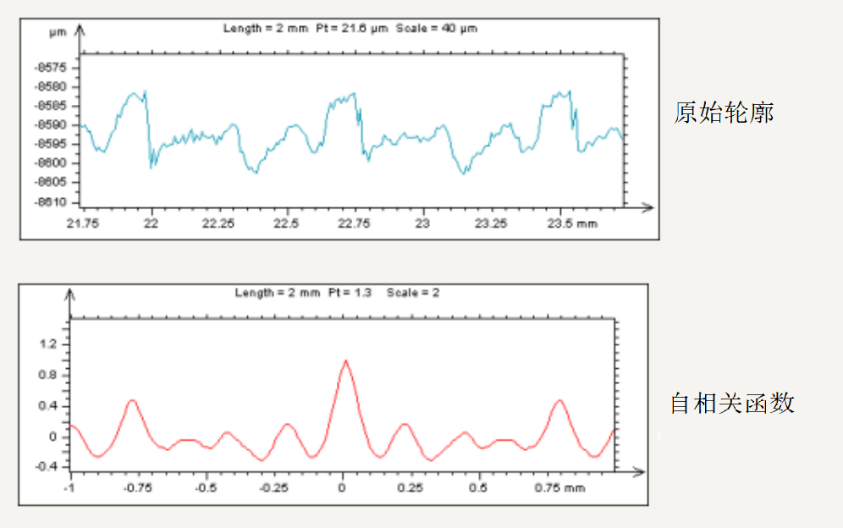
如下图所示为某一零件的剖面轮廓，具有一定的周期性，因此在自相关函数图像上可以观察到一系列极大值，它们的相对高度相对于中心叶的高度是剖面的周期性的特征。相反的，如果自相关函数图像上只有一个中心峰值，则该轮廓不具有周期性。

三、互相关函数（CCF）

（1）互相关函数简介

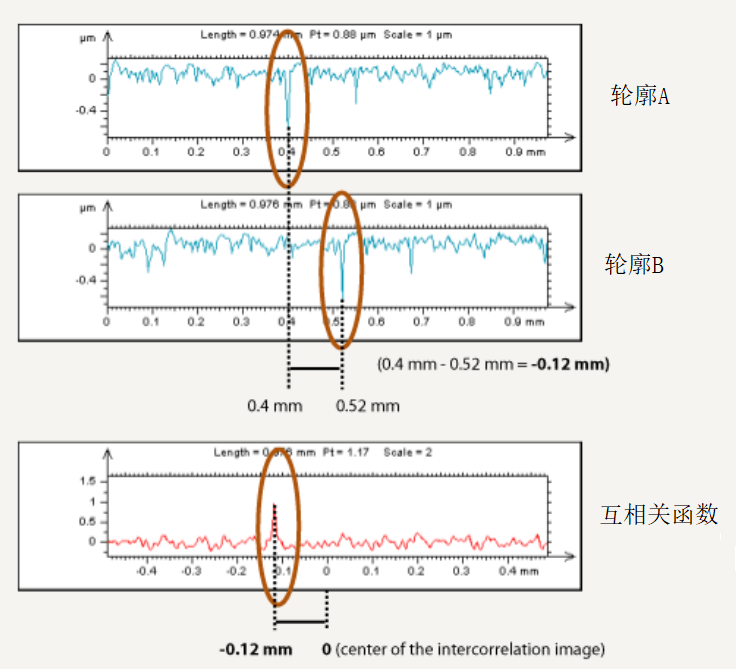
互相关函数（如下图所示）用于表面形貌的识别，互相关函数在表面形貌上的应用是用来描述一个没有位移的和另一个有横向位移的两个表面的截面轮廓之间的相似性的度量尺度，即表示两个不同轮廓波形相差一定位移时的相似程度。

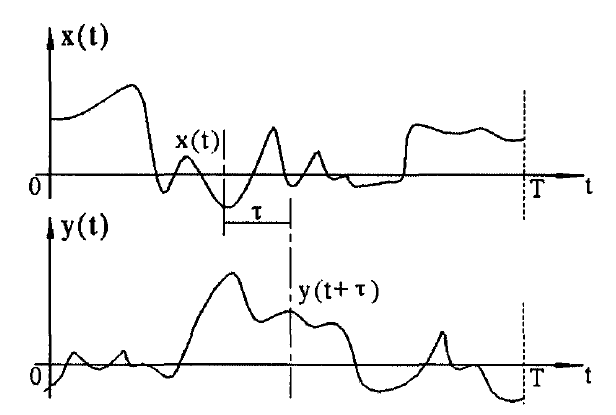
互相关函数的表达式为：

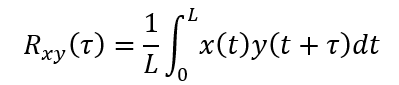
互相关函数Rxy(τ)表达了在位移上相差为τ的两个截面轮廓之间的近似程度，该函数通常不在τ=0处取峰值其峰值偏离原点的位置反映了两个截面轮廓相互间有多大位移后二者相关程度最高,即相似程度最大。

互相关与自相关的数字化估算表达式类似。当横向位移数位r,m为r中的最大值时，互相关函数的数字化估计公式为：

（2）互相关分析实例

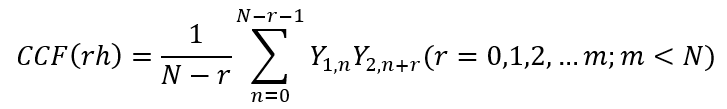
如下图所示为一组具有相对位移的剖面轮廓，位移τ大小为-0.12mm。同时在两个轮廓的自相关函数图像上原点左侧0.12mm处产生了一个峰值，反映了第二个截面轮廓向负方向产生0.12mm位移后两者相关程度最高,即相似程度最大。

四、相关系数

相关本身并不是一种确定性的关系，相关函数一般只能描述两轮廓截面的相似性，而相关程度则通常由相关系数值来表述。相关系数不是等单位量度，而是一个既没有单位名称，也不是相关的百分数的一个比率。一般情况下，可以取小数点后两位数来表示相关系数，其值前面的正负号只表示两变量的关联方向，绝对值则反映二者相关的程度。

其中，互相关系数能够反映两个轮廓截面的相关性。用付表示互相关函数值，Rxx(0)和Ryy(0)则表示在τ=0对两个不同的表面轮廓的值，则互相关系数可由如下计算表达式得到：

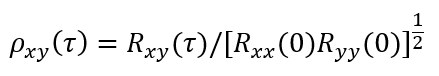
对于给定的τ值，互相关系数一般符合如下条件：|ρxy(τ)|≤1。当|ρxy(τ)|=0时，x(t)和y(t)代表的表面轮廓波形之间完全无关；|ρxy(τ)|=1则表示，x(t)和y(t)代表的表面轮廓波形是理想的线性相关；|ρxy(τ)|越接近1，两个轮廓曲线的相关程度越高。