一、光学面的定义

非球面的光学面在光学系统中是非常重要的，对于旋转对称光学面，当以Z轴为旋转轴时，可定义为

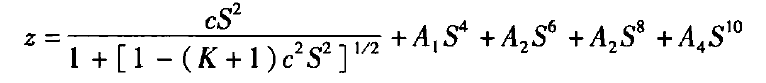
式中，S方为x方与y方之和；c为曲率半径的倒数；A（1-4）为非球面形变系数；K为二次曲线常数，是二次曲面偏心率的函数（K=-e²）。

二次曲线常数不能针对一个平面被定义。二次曲线常数的另一种表达式可根据顶点曲率半径r和由曲率中心到位于曲率中心与光学表面之间的二次光学表面焦点的距离L表述为

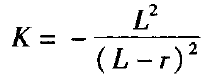
L与相应的K值对于不同的L和r的值如图1所示。

图1 二次曲率常数K图解表达式

图2为相同曲率的不同二次曲线常数的非球面轮廓。

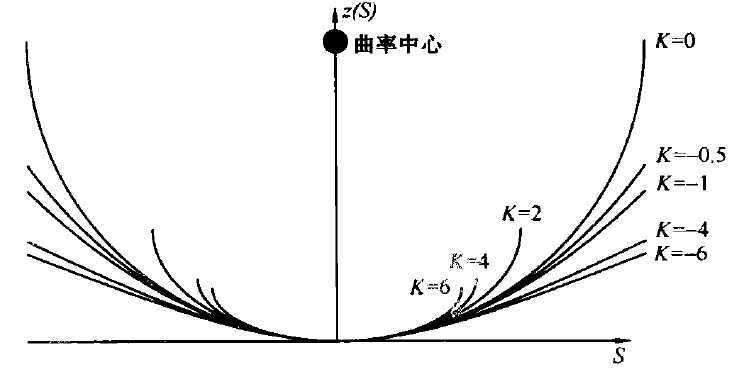
图2 相同曲率不同二次曲线常数的非球面轮廓

二、二次曲面的参数

二次曲面的焦点位置是关于r和K的函数，如图3所示。

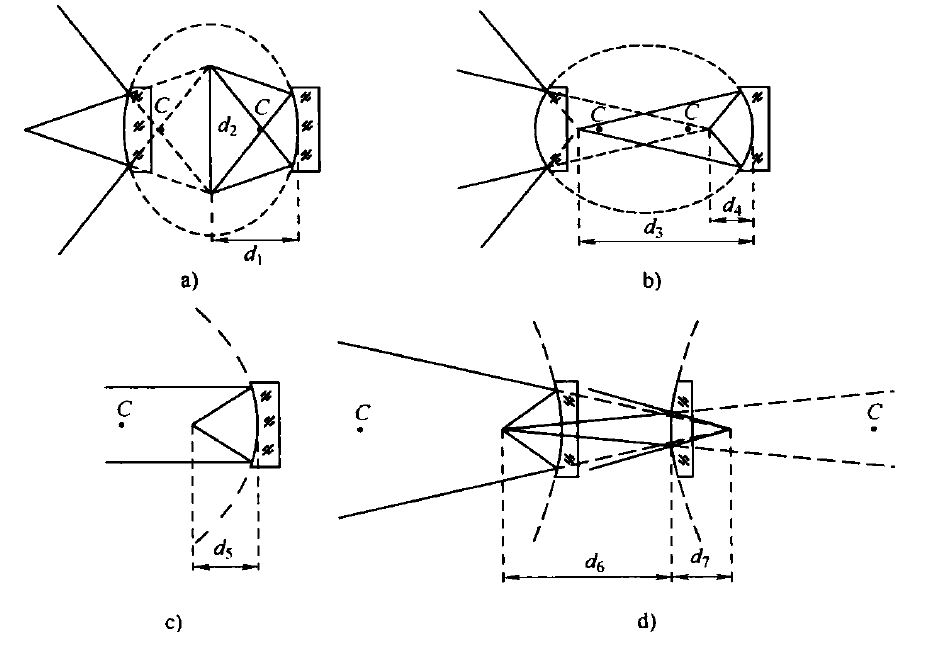
图3 二次曲面参数（C为曲率中心最高点）

a）扁平椭球面（K>0） b）椭球面（-1<K<0） c）抛物面（K>-1） d)双曲面（K<-1）

d及其关系式如下所示。

三、表面法线的像差

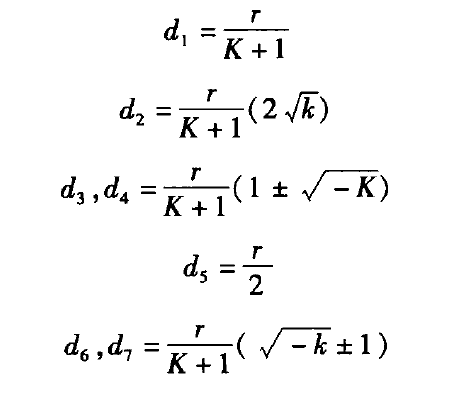
光学面的法线与光轴的交点到顶点的距离为：

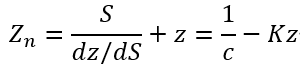
以图4的抛物面（K=-1）为例，发现误差为

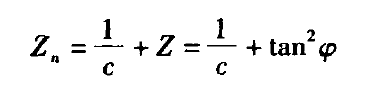
式中，角φ为平面与光轴间的夹角，如图4所示；f为抛物面的焦距。可以看到，曲率中心到光轴与法线的交点的距离Z_n与矢高Z相等，如图4在一般的非球面，法线的交点可以大致表示为

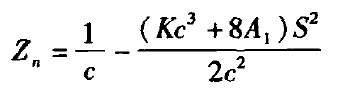
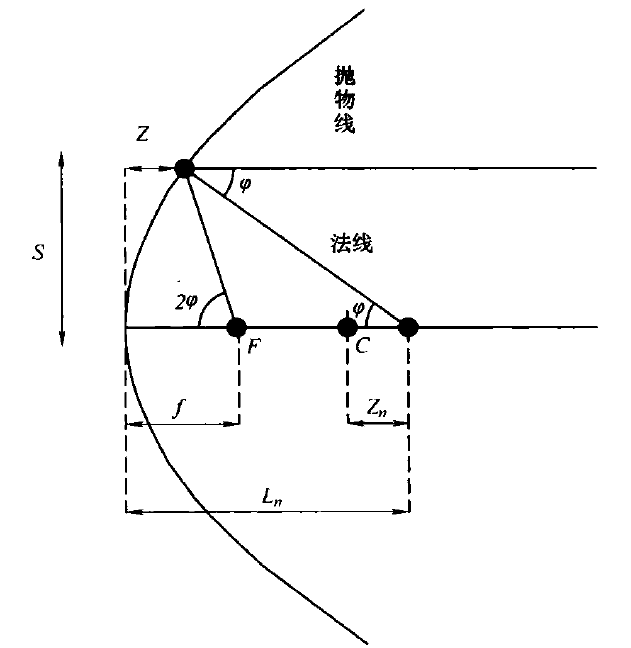
图4 凹反射抛物面