1974年Burning等人Ｗ将通讯理论中的相位探测技术引入到光干涉测量技术中，提出了相移干涉术（Phase-Shifting interferometry，PSI），通过在相干光束之间引入特定的相位偏移，产生一系列相位调制干涉图，并由此解调出待测参数，实现了高精度、实时、多参数、自动化测试，大大扩展了干涉仪的测量功能，促进了现代光学制造水平地提高。下面，分别从相移干涉的基本原理、常用移相算法、相位解包裹算法和优势等四个方面来对相移干涉测量进行简单的阐述。

一、移相干涉测量的基本原理

相移干涉测量利用干涉仪来测量两束光的相位差异，这种技术通常涉及两束光的干涉，其中一束光通过参考路径，另一束光通过测量路径，并且二者在相位上有一定的差异。相移干涉测量通过在测量路径中引入一个可控的相移来测量相位差异，一般情况下，移相式激光干涉仪中的相移可以通过控制压电陶瓷驱动器（PZT）移动参考镜位置或者改变激光器波长的方式来实现。通过改变相移的值，可以获得一系列干涉图像，然后使用算法分析这些图像，从而获得被测元件的面形信息，并根据计算好的相关参数进行质量评价（图1所示为一组移相间隔为90°的移相干涉图组）。

图1 移相间隔为90°的移相干涉图组

干涉图像中的条纹分布是由参考光束和测试光束叠加形成的干涉场导致，其干涉光强公式可由下式表示：

这就是PSI的基本公式，其中：A(x,y)是干涉图的背景光强，B(x,y)是调制度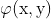，是待测物的波面初始相位信息，是移相量，(x,y)是干涉图中像素点的坐标信息。

参考镜和被测镜间的面形差P(x,y)与位相分布的关系为：

二、相移干涉测量常用的移相算法

1.四步移相算法

四步移相法是一种经典的解相算法，可以有效计算出理想移相图组的相位分布。先获取无移相的干涉图像，再进行三次移相间隔为π/2的移相，每次移相完成采集1帧图像，共得到4帧相位相差π/2的干涉图像，其图像光强信息分别为：

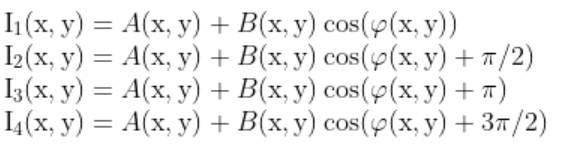
通过对上式进行处理，我们可以得到其待测相位为：

该算法求解速度快，适合对理想干涉图组进行求解。但当有外部干扰时，相位变化呈无规则态，此时四步移相法的解相效果非常糟糕，无任何抗振能力。

2.最小二乘算法

由于干涉图给定坐标上的光强变化是待测相位的正弦函数，该相位有一个已知区间和三个未知量，背景光强、调制光强和待测相位，故我们的待测相位可以通过对待测光强做一个正弦函数的最小二乘拟合来确定。

首先可将光强公式改写为：

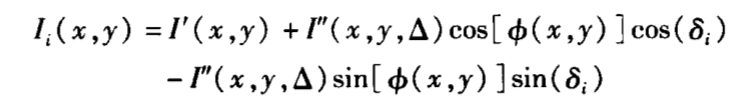
或者：

此时，

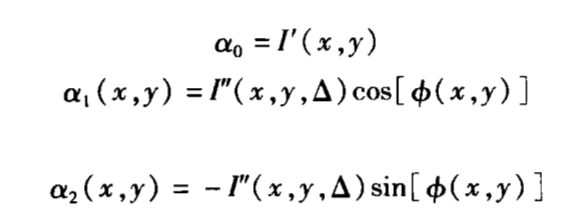
这时，测量光强和拟合光强之间的方差同三个未知量a0、a1、a2之间的关系为：

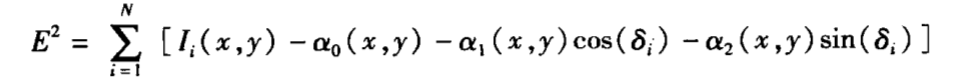
这个误差可以通过分别对这三个未知量求偏导，然后分别令其偏导结果等于零时，误差的结果最小，这三个偏导方程联立求解就能得到最小二乘的结果。

一旦三个未知量的值在每个测量坐标上被确定后，我们就可以轻易地得出待测波前相位：

三、相位解包裹算法

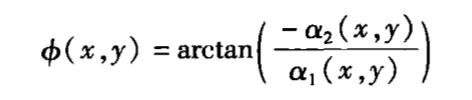
相位解包裹算法分为两类，一类是空间（空域）相位解包裹（Spatial phase unwrapping），一类是时间（时域）相位解包裹（temporal phase unwrapping）。

1.空间相位解包裹

空间相位解包裹其实就是路径跟踪方法（path-following methods）。这一类算法实际上就是在相位图中找一条最优的解包裹相位路径，是在同一个空间中进行相位解包裹的，所以称为空间相位解包裹。其经典的算法有：Goldstein枝切法、质量图导向法、掩膜切割法等。空间相位解包裹在同一张相位图中，根据某一点与其邻点的相位差进行解包裹相位，因此这种方法解包裹获得的相位被称为相对相位（relative phase map）。在解包过程中，各点运算与周围邻点有关，若某点相位解包裹错误，则其错误会传递到后续各点的运算中。

2.时间相位解包裹

时间相位解包裹是通过在不同时间得到的两个或多个不同频率的相位图来进行解包裹。它是在时间序列上通过进行解包裹的，所以称为时间相位解包裹。其经典的算法有：多频法、多频外差法等。时间相位解包裹是根据同一位置（像素）不同时间得到的相位图来进行相位解包裹，获得的相位被称为绝对相位。在解包过程中，各点运算与周围邻点无关，若某点解包错误，则错误不会传递。

四、相移干涉测量的优势

相移干涉测量有许多优势，例如高精度、非接触、无损、高灵敏度、宽测量范围和高可重复性，相比于其他测量技术，相移干涉测量可以实现更高的测量精度和更广泛的测量范围。此外，相移干涉测量还可以应用于表面形貌、光学薄膜、光学波导和光学器件等领域。